Los que me conozcáis ya sabréis que me gustan los mapas y no es la primera vez que hablo aquí de ellos. Ni siquiera es la primera entrada que hago relativa al tamaño de los territorios y las proyecciones cartográficas o sobre mapas superpuestos. La excusa que he encontrado esta vez es esta interesante herramienta que me ha dado pie a escribir este post.
Algo que ya he dicho, y no me cansaré de repetir, es que ninguna proyección cartográfica es mejor o peor que las demás, todas son visiones artificiales basadas en ecuaciones y cada una es útil con según qué propósito. Si quieres ver la realidad te recomiendo que te hagas con un globo terráqueo, pero si aspiras a ver tu planeta, o incluso parte de él, sobre una superficie bidimensional ya te advierto que estarás viendo algo que, en parte, es engañoso.

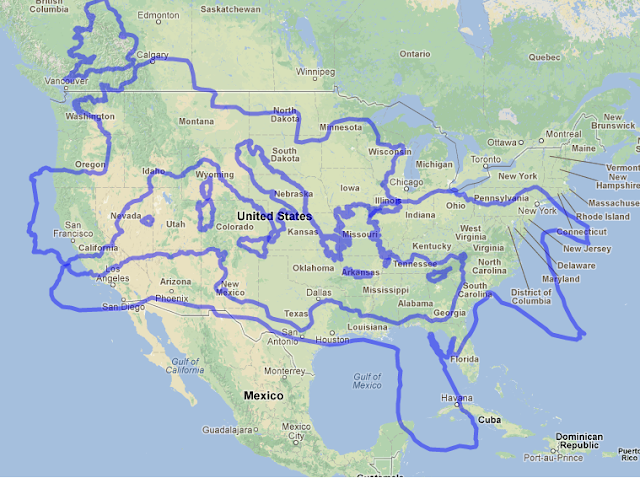
Alaska comparada con el resto de EEUU continental. Clic para verlo más grande.
El objetivo de esta entrada no es tratar el apasionante tema de las proyecciones cartogáficas aunque no está de más comprenderlas y saber que se suelen establecer clasificaciones entre las proyecciones en función de su principal
propiedad; el tipo de superficie sobre la que se realiza la proyección, plano, cilindro o cono, así como también según la disposición relativa entre la superficie terrestre y la
superficie de proyección. No voy a decir nada más (hay mucho escrito si os interesa el tema), solo que atendiendo a ello existen tres tipos de proyecciones:
- proyecciones equidistantes, si conserva las distancias.
- proyecciones equivalentes, si conservan las superficies.
- proyecciones conformes, si conservan las formas (o, lo que es lo mismo, los ángulos).
Desgraciadamente no es posible tener las tres propiedades anteriores a la vez en el mismo plano, por lo que es necesario optar por soluciones de compromiso que dependerán de la utilidad a la que sea destinado el mapa.
Una muestra de cómo "engañan" los mapas globales es la siguiente imagen. En ella se muestra la distancia más larga que se puede navegar en linea recta, desde Pakistán hasta Kamchatka. Son más de 32.000 kilómetros sin tener que mover el timón. Sobre un plano, muy recta no parece (alguno estará pensando muy acertadamente: ¡hombre claro, a mi no me la das con queso, si es sobre la superficie de la Tierra es una circunferencia!).

Así es queridos amigos, a esto se le llama navegar en línea recta. Clic para verlo más grande
Dicho esto, está claro que la proyección cartográfica sobre plano es, y ha sido, crucial a lo largo de la historia. El mundo de hoy esta marcado por líneas trazadas sobre un papel y la historia no se puede entender
sin los mapas. Eso sí, existen decenas de opciones para crear un mapa, y cada una de esas posibles proyecciones tiene sus pros y sus contras.
La Winkel-Tripel por ejemplo, está considerada la mejor proyección para representar el
mundo entero, produciendo muy pequeños errores de distancia, pequeños
errores de combinaciones de elipticidad y área, y menor asimetría estadística que cualquier otro mapa. Desde 1998 es la proyección estándar para los mapamundis hechos por la National Geographic Society. La proyección acimutal de Lambert presenta como gran ventaja que las áreas
representadas en los mapas no sufren deformación y son proporcionales a
las formas originales, cumpliéndose la regla siguiente: "superficies iguales representan ángulos sólidos iguales". La proyección de Mollweide facilita la representación de toda la superficie terrestre con menos deformación en las áreas polares que la proyección cilíndrica y con gran fidelidad en las áreas cercanas al ecuador. Su principal desventaja es que las áreas cercanas a los bordes aparecen deformadas. La proyección usada por google, contra la que no tengo nada y es quizá la más conocida por todos, es la Mercator, que revolucionó la cartografía y fue muy útil para la navegación en el momento que fue creada.
Pero a pesar de ser la más extendida la proyección Mercator no es buena para comparar tamaños, sobre todo si los tamaños a comparar se encuentran en latitudes muy dispares. Un caso paradigmático es el de llevar Groenlandia hasta un lugar cercano al ecuador. Nadie ha encogido nada en la imagen siguiente, la extensión de Groenlandia se ha mantenido, solo que adquiere un tamaño diferente según la zona del plano sobre la que la representemos. Aquí sobre Australia, por ejemplo.

Se rumorea que esta fue la primera versión de la carátula de la película Cariño, he encogido a los niños.
Cuanta mayor sea la latitud a la que se encuentra más grande parecerá un territorio, luego territorios muy cerca o sobre el ecuador dan la sensación de ser menores de lo que son. Fíjate en el tamaño de Brasil al superponerlo con Europa o Norteamérica.
Brasil superpuesto sobre Europa (y África). De Libia a Islandia pasando por Moscú.
Brasil superpuesto sobre Norteamérica. Descontando Alaska sería mayor que EEUU.
Podemos hacer el viaje en sentido contrario y llevar un país europeo, en este caso Alemania, hasta Sudamérica. El tamaño de la potencia económica centroeuropea en este contexto puede sorprender a más de uno.
La provincia de Buenos Aires es solamente 50.000 km² menor que Alemania, que, a su vez, es
aproximadamente el doble que Uruguay. Eso sí, en población golea Alemania.
aproximadamente el doble que Uruguay. Eso sí, en población golea Alemania.
Veamos el caso de Chile, que con su singular geografía podría conectar Túnez, casi casi, con el archipiélago Svalbard. Y si te apetece, podés comparar Argentina (y sí, así se vería si estuviese a la latitud de Canadá, la deformación que se ve es debida a la proyección utilizada).
No me quiero imaginar el precio a pagar en una autopista de peaje chilena para ver el país "de arriba a abajo".
Colombia con sus 1.138.910 km² sería, de largo, el mayor país de Europa por extensión (si no entrase Rusia en la lista, claro). Perú estaría ligeramente por encima. Por no hablar de La India o Australia.
Colombia superpuesto sobre la península ibérica.
Perú, nuevo megaestado europeo.
El tamaño de la India es de 3,3 millones de km². La UE tiene 4,3 millones. Australia 7,7.
Otros países,en cambio, son realmente pequeños. La Ciudad del Vaticano es el estado de menor extensión del planeta. Como puedes ver a continuación es sensiblemente menor que el Parque del Retiro de Madrid, que a su vez es sensiblemente menor que el neoyorkino Central Park. Ya sé que esto se puede ver en cifras en la wikipedia por ejemplo, pero de la siguiente manera es más visual.
La Ciudad del Vaticano superpuesta sobre el Parque del Retiro de Madrid.
El Central Park de Nueva York en Madrid.
Y ya puestos podemos ir un poco más allá y comparar grandes extensiones históricas que en el pasado formaron un solo ente de alguna forma. Se me ocurre la Gran Colombia, el imperio mongol o el romano, que puedes ver a continuación.
Imperios de ayer y hoy superpuestos
En MAPfrappe puedes hacer tus propias comparaciones. Algunas ideas pueden ser Japón - Europa, Manhatan - Barcelona, España por el mundo, UE - Australia....
Tampoco dejes de visitar el blog de MAPfrappe donde comparan todo lo comparable.
Por cierto, ¿cuál es tu proyección cartográfica favorita?











Muy currado. Australia ya se ve algo deformado sobre Europa por el tema de Mercator, tenías que llevarla más al norte para ver la deformación a lo bruto. Quien dice Australia dice cualquier otro país eh.
ResponderEliminarGracias Jorge. Traté de no llevarlos a latitudes muy altas para que se viese claramente de que país se trataba, jeje. Cuando pones algo sobre Canadá sale un monstruo que asusta.
ResponderEliminarInteresantísimo. ¡Gracias!
ResponderEliminarTe dejo una página con un juego en el que recolocar 15 países mal situados en mapamundi con proyección Mercator:
ResponderEliminarMercator Puzzle
Sobre la entrada, aunque se queda corta, muy interesante.
Fdo: Un fan de los mapas.
@Milhaud, gracias por el regalo, aunque tengo que decir que me topé con él hace unos días, por reddit, creo. Pero he vuelto a jugar :D
ResponderEliminarFdo: Un fan de Mapas Milhaud y Recuerdos de Pandora
Si recorres Chile de Arica a Puerto Montt (2700 km) te costará 85 euros. Eso corresponde al 60-65% de la longitud de Chile. El resto no se puede hacer por tierra.
ResponderEliminar@Hannibalito, gracias por el dato, que grande.
ResponderEliminarMe parece un precio muy competitivo, a mi los 150 km Vigo-A Coruña me cuestan 30 euros (ida y vuelta)
Lo he flipado con varias cosas pero lo que más me ha sorprendido es el mapa de la linea recta navegable más larga.
ResponderEliminarLa imagen "Cariño, he encogido a los niños" es muy sorprendente. La entrada es excelente para los no iniciados.
ResponderEliminarHola Excelente me encanta la Historia Te dejo una web donde podemos compartir informacion matematica, fisica, quimica, Historia, Trigonometria, Muy Buen Blog.
ResponderEliminarwww.resolviendo.co
muuuuy bueno!!
ResponderEliminarNavegando por ortodromica el rumbo, por tanto el timón, tienes que ir variando a medida que recorres dicha ortodromica.
ResponderEliminarExtraordinario blog.
muy buenas las comparaciones! te felicito, solo una cosa que criticar: en el mapa de Brasil también incluiste al Uruguay!!!! eso es imperdonable
ResponderEliminarun uruguayo
@Juan Pablo, vaya, tienes razón, y también incluía Guyana Francesa. Bueno, realmente se trataba de un mapa de Uruguay con algunas anexiones ;-)
ResponderEliminarCorregido.
Alfred Crazy comenta : muy buena está página y llevada con humor para aligerar
ResponderEliminarla carga . Lo que no me cae bien es que frente a los que no saben un pito de la
materia , dejes a MERCATOR tirado a un costado. Para los marinos , el ingenio
de ese hombre, no tiene precio.
Hola! Muy interesante tu artículo, yo también tengo varios posts parecidos en mi blog. ¡Saludos y felicitaciones por el blog!
ResponderEliminarMuy chévere tu información, gracias por compartirla
ResponderEliminarLa silueta de Brasil NO incluye al Uruguay NI a la Guyana Francesa. Apréndanse mejor la la silueta de sus países.
ResponderEliminar